Presentation - Semantic Daniélou

by Jacques Dudon

After having a tunable keyboard-based instrument made by Maurice Martenot in 1936, and several microtonal harmoniums during his later travels throughout India, Alain Daniélou designed a new electronic instrument in 1967 called the S52 and commissioned its development to Stefan Kudelski of Lausanne, Switzerland, the inventor and creator of the Nagra, the famous high quality portable tape-recorder. Stefan Kudelski entrusted the project to his son André, a young electronics engineer, and to Claude Cellier, an electronics engineer and musician. The instrument was modelled exactly on the system presented in the book “Sémantique Musicale” and was technically highly elaborated. Although it presented a few shortcomings, it enabled Alain Daniélou to advance with his theory which was inspired from the Indian model, and to test its psychoacoustic applications. The prototype was presented in Paris in 1980 to the UNESCO International Music Council as well as the IRCAM (Institut de Recherche et Coordination Acoustique/Musique), and afterwards in Bordeaux, Berlin, Rome, etc.

It was not however until 1993 that the idea of the first instrument using only digital technology came into being. The Semantic-36, named by the composer Sylvano Bussotti, was developed by two professional computer music engineers who were greatly interested in the work of Alain Daniélou. Michel Geiss, at the time electronics engineer, musician, collaborator of Jean Michel Jarre and electronic instrument design specialist, took charge of the project and developed the keyboard, with the help of Christian Braut who elaborated the MIDI programming system, the sounds and the scales. Other collaborators in the project were Jean-Claude Dubois, who developed the operating system, and Philippe Monsire, who was behind the futuristic design of the instrument. The Semantic-36 was delivered a few years later, but Alain Daniélou died on the 27th January 1994 without having seen the finalised instrument.

There was only one existing model of the instrument, which I had the honour of using throughout 2007 at our AEH research centre area, for a number of musical experimentations and creations. The Semantic Daniélou was essentially a microtonal keyboard with 36 sounds per octave, containing on the same horizontal surface two Cavagnolo MIDI button keyboards for electronic accordion, connected to a sampler specially reprogrammed according to just intonation. Its tuning followed the same tonal framework as the S52 and previous keyboard – an extension of the 22 shrutis used in both the North and South of India, and thus it offered an intermediate subset between the 22 shrutis and the global Semantic system of 53 sounds per octave.

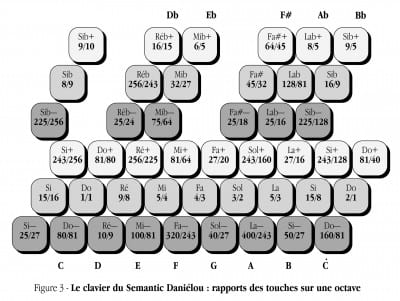Figure 3 shows the sound ratios selected by Alain Daniélou for the 36 keys and their mapping (with French note names). On either side of the rows which correspond with the “white” and “black” traditional western keyboard notes, are additional keys, which raise (+ sign) or lower (- sign) the notes by a syntonic comma. The instrument was also equipped with a pitchbend in the form of a ribbon controller. The sounds were generated by a sampler (Kurzweil K2000) and were chosen for their simplicity and for their harmonics which were exclusively multiples of numbers 2/3/5 – which, according to its developers, respected Daniélou’s vision by enhancing the consonance and purity of the intervals.

The particularity of the Semantic-36, which was not conceived for chord changes, was that it offered a precise sensory experience involving exclusively the consonances and harmonies that arise from harmonics 2, 3 and 5, which – apart from harmonic 2 – are absent in the equal temperament. By offering a choice of three pitches per chromatic degree, the Semantic-36 scale required a certain degree of knowledge of just intonation, which our current approach to music accustomed us to dismissing. Although the perfectly octavial structure of the keyboard allowed the player to immediately reproduce the octave intervals, the correct interpretation of all the other intervals required a prior knowledge, if only to memorise their positions. Beginners, for example, were surprised to discover that in order to obtain the exact fifth (A+) of D, they had to change rows and raise the A by a comma, whilst the other six notes had their fifth in the same row. Beginners who were familiar with the book “Sémantique musicale” may have objected to the fact that this central diatonic row positioned alongide each other notes which belonged to different series; four of them being from the same cycle of fifths (F, C, G and D) whilst the three others (A, E and B) being transpositions of factor 5, which it may have seemed logical to place on the lower row. This was however not possible for several reasons. Firstly because the series of different families have less than 12 notes, and also due to the fact that this would have favoured a”pythagorian” diatonic scale (generated from factor 3), which would have emphasised other tonics instead of the very natural diatonic limit-5 scale chosen here by Alain Daniélou in C, the reference key of his system. If we consider rows 2 and 5 together (the “white” and “black” central notes), we note that these twelve notes follow a continual cycle of fifths (with a single schisma difference between 45/32 and 256/243), starting on the A (5/3) and ending on the D (9/8). In order to complete the cycle, the use of a fifth lowered by a comma was unavoidable. This was the reason that the layout of the keyboard, in the 5-harmonic limit with C for reference, was the only possible option for this type of instrument, and that the A was not the pure fifth of the D. For other intervals this type of irregularity was even more frequent. However, once familiarised with the layout of the chords, it became easier to navigate throughout this new scope of pitches and express all their musical qualities.

It can only be pleasing to the ear to perceive a larger number of intervals, that is, as long as they are just and coherent. On the other hand, a certain degree of dexterity was required in order to master the keyboard fingering of the Semantic-36. The price to pay for the increased musical richness was inevitably a greater difficulty mastering its use. Even basic scales with one or two sharps or flats for example, could be difficult to play in some circumstances, and certain transpositions would have been welcome, but the original instrument, such as it was designed, did not allow the player to retune it in this way: the layout of its keyboard restricts its use to the key of C alone. Experiments carried out on the Semantic Daniélou prototype gave rise to new conceptions of the instrument, using computerised techniques to simplify its use, such as the possibility of integrating settings so that the keys play the sounds of different notes, which could be selected amongst the sounds of the system (or any other system). In this way the unused notes in a given piece could be replaced by duplicates of useful notes, to reduce the risk of playing wrong notes as well as improving the position of the notes in terms of fingering. All this would have required was to memorise the programmed configurations so that they were available for use whenever needed, which would provide a very efficient and educational tool, adaptable for all kinds of music.

As far as Alain Daniélou’s choice of intervals for the Semantic is concerned, his selection was one of the best possibilities given the inevitable schismic alternatives that come with such a large number of notes, starting with the 22 shrutis. This particularity did not however warrant increasing the number of keys in order to access these schismas. The system of personalised scales as mentioned previously enabled this without needing to modify the keyboard. “Depending on the chords, it is possible to choose the variations obtained by different cycles of fifths, such as limmas 256/243 or 135/128 (difference of 2 cents)“. This is what Alain Daniélou wrote of the S52, with his very clear intention of preserving the precise value of the selected notes, even though a slight temperament between the double notes would have provided a possible solution. This enables us to qualify the Semantic’s system of just intonation not only as “commal” but also of “virtually schismic”. I would like to highlight here an interesting choice by Alain Daniélou concerning the D+ key, for which, instead of the last fifth of the 1/5 family, D+ 729/640, he preferred the D+ 256/225, the only one belonging to the family 1/5², as if his intention was to remind us that this 36-sound scale is not an end in itself, but part of a greater set, notably in relation to the powers of 5.

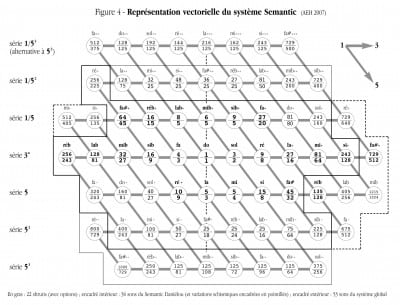Figure 4 describes, in vector format (with French note names), the origins of the different sounds of the Semantic system. This graphic representation is essential in understanding the harmonic relationships between these sounds with regards to factors 3 and 5, i.e. the “expressive” components of their intervals. Factor 2 is not represented and all the ratios are reduced to between 1 and 2.

Each horizontal movement of a vector unit towards the right (for example from C to G) indicates a transposition of a fifth (3/2), or in other words, harmonic 3 of the initial sound, transposed to the original octave (between 1/1 and 2/1). A downward diagonal movement (for example from C to E) indicates a transposition of a major third (5/4), which is harmonic 5 of the initial sound, transposed down to the original octave. Any angle could have been given to the harmonic 5 vector, but it was chosen pointing downwards, firstly to echo the commal base rows (-) of the Semantic keyboard, on which it is omnipresent, and also to vertically align the symmetrical axis (125/108 – 25/18 – 5/3 – 1/1 – 6/5 – 36/25) of the central points of the Semantic’s 6 families of sounds. The central box includes the 36 notes of the Semantic Daniélou, and as can be seen, it spans approximately four of the six families.

All the intervals are thus represented geometrically with a precise vector, whose displacement to a different point on the matrix signifies the transposition of this interval. The possibilities of displacement of this vector within all the points of a given scale determines the number of occurrences of this interval in the scale. This enables the player to immediately find all the possible transpositions of an interval, or therefore of a chord, a scale, etc. in a given set. To give a very simple example, if we look at the set of points C D E F G A B, they are characterised by a specific form which gives us their identity, and we can already see that it contains three perfect triads (= triangles formed by C E G). By displacing this structure, we are then able to discover all its possible transpositions inside a larger set, for example the 22 shrutis, etc. (it may be helpful to use tracing paper or a transparent sheet onto which the chosen structures can be drawn).

Let us now consider the vector of the syntonic comma (81/80). It is located between 1/1 and 81/80 (or between the shrutis 5/3 and 27/16, etc.), at the end of a suite which includes, in the order we prefer, 4 ascending fifths (3/2) and a descending major third (5/4) (an inverted 5/4 vector). Its possibilities of displacement between all the points of the inner box in figure 4 (which corresponds with the 36 sounds of the Semantic Daniélou-36) shows us each occurrence of the syntonic comma in this set, of which there are 18. Where then are the six missing commas, in order to reach the total of 24 on the keyboard? They are simply a different type of comma, just like the one that separates F# (45/32) from F#+ (64/45), i.e. 2048/2025, and their positions can be found in the same way, via their displacements.

To provide a final example, the vector of the schisma is found between 256/243 and 135/128. It is therefore easy to find the schismic doubles of all the given notes, of which only a few are represented within the dotted border of the box each side of the initial notes. How many schismas do the sets of the Semantic with 36 or 53 sounds contain? Zero, naturally, since neither system includes double notes which differ by a schisma, and whose borders (as seen in figure 4) are thus defined in width by this vector. It is important to note that the number of shrutis, shown here in bold, is 24, in order to demonstrate two very common schismic options (135/128 and 729/512) possible with the shrutis mentioned by Alain Daniélou — although the so-called “22” shrutis, in regards to their schismic variants, could in fact be more numerous.

One of the advantages of this vector representation is that it makes it easier to count and classify the number of identical intervals contained in a set of notes. The interval which is the most present on the Semantic Daniélou-36, after the octave, is the fifth 3/2 (or inversely the fourth), with 31 occurrences. These fifths, completed by 4 fifths lowered by a schisma, together create a continuous cycle of 35 fifths from A— to D+. After the fifth is the major tone 9/8 (or its complement the seventh 16/9) with 27 occurrences, followed equally by the major third 5/4 (and the minor sixth 8/5), with 25. We can also note that the two minor thirds 6/5 and 32/27 come next jointly with 23 occurrences, but if we count the schismic double of 32/27 (i.e. 1215/1024), which appears 10 times, we can consider the shruti 32/27 as the main minor third. We can also observe that the limma Db left us understandably undecided since it appears 16 times in its major form 135/128 and 15 times in its minor form 256/243, whatever the choice of limma stemming from 1/1. In the same way we can also trace in the rarer intervals of the system, in order to locate them on the keyboard and test them.

In this way the vector representation allows us to clearly determine the harmonic origin of each interval, the structure of all the scales, as well as their potential transpositions and variations, in the finest of detail. On the other hand, it does not give us a direct visual indication of their size, but figure 5 provides this information since it shows all the notes of the global system, this time along a circle, whose circumference is equivalent to a logarithmic octave (ie. 1200 cents, if we use this unit of measurement). “Logarithmic” here means a representation of the intervals according to their relative dimensions. One same interval is represented everywhere by the same circular arc angle, whatever its position in the octave, with the additions or subtractions of arc angle representing the corresponding multiplication or division of their pitch ratios. The ratios of the 12 central keys of the Semantic Daniélou-36 are shown in bold, with their note names. Along with their neighbouring notes, indicated by a – or + sign, they represent the 36 sounds of the instrument.

These 12 basic chromatic notes are separated by two types of semi-tones, 7 limmas and 5 apotomes according to the classic tetrachordal pattern as follows: L A L L A – L A L L A – L A. These 12 semitones are each ultimately divided into 4 or 5 “commas”, among which there is one larger comma, here bigger in size and coloured grey, called a “disjunction”. The limmas are thus composed of 3 commas and a disjunction, and the apotomes of 4 commas and a disjunction.

Where do these disjunctions come from? The notes of Alain Daniélou’s system follow a specific hierarchy (figure 4) stemming first of all from a central “chromatic core” of 12 notes, which can be extended to other notes which differ from the first ones by a comma, and so on and so forth. This is how we go from 12 basic notes to the 22 shrutis, and then to the 36 notes of the Semantic Daniélou-36, and finally to the 53 notes of the entire system, with which the whole soundscape is filled. The interval remaining in the middle of each of the 12 semi-tones which are reduced successively by three or four commas, is a larger comma. It is a complex interval since it connects families of opposite extremes in terms of powers of 5, and has again here, with the same eternal distance of a schisma (1,95372 cent), two different expressions: 20 000 / 19 683 or 3 125 / 3 072. The first reads 27,66 cents and appears seven times, the second 29,61 cents and it appears five times. Given that the commas are themselves doubles (of 21,50 or 19,55 cents), these disjunctions measure on average 4/3 of an average comma.

As we have just seen for the limmas and apotomes, we can also use the octave circle to measure and compare, down to the precision of a schisma, the dimensions of all the intervals of the system by counting the number of commas + disjunctions they are made up of. In this way we can calculate that a minor third 32/27 is made up of 10 commas + 3 disjunctions, and we can apply the same process to any interval we wish. A fourth is composed of 17 commas + 5 disjunctions, the only exception being found between F# – – and Bb + +, where we count 18 commas and 4 disjunctions, making this the rarest interval of the system, along with its complement, the “wolf fifth”, located between Bb + + and F# – – , and measuring 708,11 cents. We can verify on the vector representation in figure 4 the singularity of these two intervals which form a diagonal, and are not transposable and offer no possible schismic variation, along the perimeter of 53 sounds. We can note that the cycle of fifths cannot loop back over itself after the 53 sounds of Alain Daniélou’s system, without there being a gap of a third of a comma (a kleisma of 15 625 / 15 552), which it is preferable to integrate in order to make the Bb + + as correct a fifth as any of the others. This 54^th note is an F + + which can be either 2 187 / 1 600 or its double 512/375, chosen here to imitate Alain Daniélou’s choice of 256/225 for the Semantic keyboard.

This F ++ having been added, we can now enter the labyrinth by means of ascending or descending paths, the end of both leading – providing the middle route is always chosen – to another note on the circle, a fourth higher or lower. We can also shorten this long path by branching off to other intervals, for example by switching half way along, where we see two intermediary, clearly visible circles, which trace the limits of the major second (9/8) and major third (5/4) intervals. All of these paths are possible, and we can of course also end up finding ourselves lost, which is the advantage of labyrinths, to set out in search of the rarest intervals, or most irregular in terms of their number of disjunctions, which will lead us to the harmonic boundaries of Alain Daniélou’s system.