Par Jacques Dudon
Après avoir fait réaliser en 1936 un instrument à clavier accordable par Maurice Martenot, puis, au cours de ses voyages en Inde plusieurs harmoniums microtonaux, Alain Daniélou conçoit, en 1967, un nouvel instrument électronique, le S52, dont il demande la réalisation à Stefan Kudelski, de Lausanne, inventeur et fabricant du Nagra, le fameux magnétophone portatif haut de gamme. Ce dernier confie cette tâche à son fils André, jeune ingénieur électronicien et à Claude Cellier, lui-même électronicien et musicien. L’instrument, exactement basé sur le système exposé dans la « Sémantique Musicale » et techniquement très élaboré, présente quelques défauts, mais permet à Alain Daniélou d’avancer dans sa théorie, inspirée du modèle indien, et d’en vérifier les applications psychoacoustiques. Le prototype sera présenté en 1980 à Paris, entre autres au Conseil international de la musique de l’UNESCO, mais aussi à l’Ircam, puis à Bordeaux, Berlin, Rome, etc.
Il faudra attendre cependant 1993 pour que prenne forme l’idée d’un premier instrument cette fois de technologie entièrement numérique, le Semantic, baptisé ainsi par le compositeur Sylvano Bussotti, qui sera réalisé par deux professionnels de l’informatique musicale passionnés par les travaux d’Alain Daniélou. Michel Geiss, alors électronicien, musicien et collaborateur de Jean Michel Jarre et spécialiste de la lutherie électronique, prend la conduite de ce projet et conçoit les claviers, épaulé par Christian Braut qui prend en charge la programmation du système MIDI, des sons et des échelles. Participent également au projet Jean-Claude Dubois, qui réalise le système d’exploitation, et Philippe Monsire, qui signe le design très futuriste de l’instrument. Le Semantic sera achevé quelques années plus tard, mais Alain Daniélou meurt le 27 janvier 1994 sans en avoir vu l’aboutissement.
Il n’existe à ce jour qu’un exemplaire de cet instrument, que j’ai eu l’honneur d’accueillir toute l’année 2007 dans notre centre de recherches (l’Atelier d’Exploration Harmonique) pour diverses expérimentations et créations musicales. Le Semantic Daniélou est essentiellement un clavier microtonal à 36 sons par octave, rassemblant sur une même surface horizontale deux claviers-boutons MIDI Cavagnolo pour accordéon électronique, connectés à un échantillonneur spécialement reprogrammé en intonation juste. Son accord suit le même canevas tonal que celui du S52 et des claviers précédents, une extension des 22 shrutis utilisés en Inde du Nord comme du Sud, et constitue ainsi un sous-ensemble intermédiaire entre les 22 shrutis et le système Semantic global à 53 sons par octave.
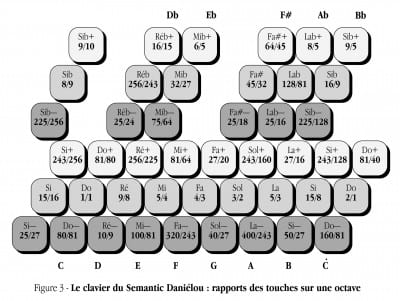 La figure 3 détaille les rapports des sons des 36 touches du clavier sélectionnés par Alain Daniélou et leur agencement. Au-dessus et au-dessous des rangées centrales des “blanches” et des “noires” du clavier occidental traditionnel sont déployées des rangées de touches complémentaires, haussant (signe +) ou baissant (signe -) les notes d’un comma. L’instrument possédait aussi à l’origine un “pitch bend” (levier de glissando) sous la forme d’un “ribbon controller”. Les sons sont générés par un échantillonneur (Kurzweil K2000) et ont été choisis parmi les plus basiques et dépouillés qui soient — notamment avec des harmoniques seulement multiples des nombres 2/3/5 — afin, selon les concepteurs, de rester en accord avec la vision de Daniélou et de mettre en valeur la consonance et la pureté des intervalles.
La figure 3 détaille les rapports des sons des 36 touches du clavier sélectionnés par Alain Daniélou et leur agencement. Au-dessus et au-dessous des rangées centrales des “blanches” et des “noires” du clavier occidental traditionnel sont déployées des rangées de touches complémentaires, haussant (signe +) ou baissant (signe -) les notes d’un comma. L’instrument possédait aussi à l’origine un “pitch bend” (levier de glissando) sous la forme d’un “ribbon controller”. Les sons sont générés par un échantillonneur (Kurzweil K2000) et ont été choisis parmi les plus basiques et dépouillés qui soient — notamment avec des harmoniques seulement multiples des nombres 2/3/5 — afin, selon les concepteurs, de rester en accord avec la vision de Daniélou et de mettre en valeur la consonance et la pureté des intervalles.
La spécificité du Semantic, qui n’est pas conçu pour changer d’accord, est donc bien de permettre une expérience sensorielle précise, celle des consonances et harmonies offertes par les harmoniques 2, 3 et 5 exclusivement, qui sauf pour l’harmonique 2 sont absentes du tempérament égal. En proposant à cet effet un choix de trois hauteurs par degré chromatique, l’échelle du Semantic requiert une certaine initiation à l’intonation juste, dont les pratiques musicales courantes nous ont habitués à nous dispenser. Si la structure parfaitement octavielle du clavier permet la reproduction immédiate des intervalles d’octave, l’interprétation correcte de tous les autres intervalles demande l’acquisition préalable d’une compréhension, sinon d’une mémoire de leurs positions. Le néophyte pourra être par exemple étonné de constater qu’il faut changer de rangée et hausser le La d’un comma pour obtenir la quinte exacte (La+) du Ré, alors que les six autres notes trouvent leur quinte dans cette même rangée. Un autre néophyte, qui aurait lu Sémantique musicale, pourrait quant à lui objecter que cette rangée diatonique centrale aligne des notes de séries différentes, puisque quatre sont issues du même cycle de quintes (Fa Do Sol Ré) tandis que les trois autres (La Mi Si) en sont des transpositions par le facteur 5, qui auraient pu être ainsi alignées sur la rangée inférieure. Mais cela n’était pas possible pour plusieurs raisons. D’une part parce que les séries des différentes familles ont moins de 12 notes, d’autre part cela aurait privilégié une échelle diatonique “pythagorienne” (issue du facteur 3), favorisant d’autres toniques, au lieu de l’échelle diatonique de limite 5 très naturelle choisie ici par Alain Daniélou dans la tonalité de référence de son système, en Do. Quand on considère l’ensemble des rangées 2 et 5 (notes “blanches” et “noires” centrales), on s’aperçoit que ces douze notes suivent (à un seul schisma près entre 45/32 et 256/243) un cycle continu de quintes partant du La 5/3 pour aboutir au Ré 9/8. Pour finir ce cycle une quinte faible d’un comma était inévitable, et donc cette partition où le La n’est pas la quinte du Ré, en limite harmonique 5 avec un Do comme référence était la seule option possible avec ce type de clavier. Pour d’autres intervalles, ce genre d’irrégularités y était encore plus fréquent. Cela étant, une fois reconnue l’arborescence des accords, il était possible de retrouver son chemin à travers cette nouvelle richesse de hauteurs, pour en exprimer toutes les qualités musicales.
L’oreille ne peut trouver à priori que du plaisir à percevoir un plus grand nombre d’intervalles, tant que ceux-ci sont justes et cohérents. En revanche, le déplacement des doigts sur un tel clavier exige une dextérité particulière et le prix à payer pour ces nouvelles ressources tonales était bien sûr une plus grande difficulté de jeu. Une échelle même basique, mais ayant seulement un ou deux dièses ou bémols par exemple, pouvait se montrer difficile à jouer et certaines transpositions étaient bienvenues, que l’instrument original hélas ne permettait pas de réaccorder : la logique de son clavier le restreignait alors à la seule tonalité de Do. Les expérimentations effectuées sur ce prototype du Semantic Daniélou nous permettaient cependant d’envisager de futures versions de l’instrument, qui feraient appel à des techniques informatiques pour en faciliter l’approche gestuelle. Une idée était de pouvoir affecter aux touches de son choix d’autres notes, sélectionnables parmi la palette globale des sons du système (ou de tout autre système). On aurait pu ainsi remplacer les notes non utilisées dans telle ou telle échelle par des doublons des notes utiles, afin d’éviter des fausses notes et d’optimiser la position des notes en regard de leur doigté. Il suffisait alors de pouvoir mettre en mémoire les configurations programmées, afin d’en disposer au moment voulu, pour avoir là un outil très pédagogique et performant au service de toutes sortes de musiques.
Concernant le choix des intervalles effectué par Alain Daniélou pour le Semantic, c’est un des meilleurs possibles, compte tenu des inévitables alternatives schismiques que présentent un grand nombre de notes, à commencer par plusieurs des 22 shrutis. Celles-ci ne sauraient justifier d’augmenter le nombre des touches pour disposer de ces schismas, ce que permettrait par contre sans modification du clavier un système d’échelles personnalisables comme celui que je viens de suggérer. “Il est possible de choisir selon les accords les variantes obtenues par les différents cycles de quintes tels que les limmas 256/243 ou 135/128 (différence 2 cents) .” Ainsi Alain Daniélou écrivait-il, à propos du S52, son intention très claire de garder intacte la valeur précise des notes choisies, alors qu’un infime tempérament entre les notes doubles aurait pu régler la question. Ceci nous permet de qualifier le système d’intonation juste du Semantic, non seulement de “commal”, mais aussi de “virtuellement schismique”. Je signalerai ici un choix intéressant d’Alain Daniélou, pour la touche Ré+, à laquelle au lieu de la dernière quinte de la famille 1/5, Ré+ 729/640, a été préféré un Ré+ de 256/225, le seul représentant de la famille 1/5^2, comme pour nous rappeler que cette échelle à 36 sons ne s’arrête pas là, et fait partie d’un ensemble plus grand, notamment sous l’aspect des puissances de 5.
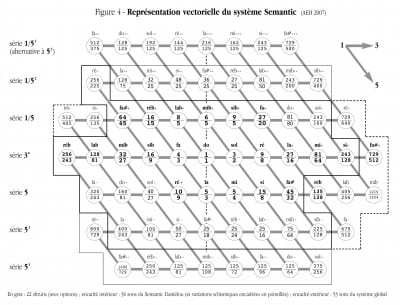 La figure 4 détaille, sous forme vectorielle, la genèse des différents sons du système Semantic dans sa configuration d’origine. Cette représentation graphique est indispensable pour pouvoir comprendre les relations harmoniques de ces sons en regard des facteurs 3 et 5, c’est-à-dire les composants “expressifs” de leurs intervalles. Le facteur 2 n’est pas représenté et tous les rapports sont ramenés entre 1 et 2.
La figure 4 détaille, sous forme vectorielle, la genèse des différents sons du système Semantic dans sa configuration d’origine. Cette représentation graphique est indispensable pour pouvoir comprendre les relations harmoniques de ces sons en regard des facteurs 3 et 5, c’est-à-dire les composants “expressifs” de leurs intervalles. Le facteur 2 n’est pas représenté et tous les rapports sont ramenés entre 1 et 2.
Un déplacement horizontal d’une unité vectorielle vers la droite (par exemple de Do à Sol) indique une transposition d’une quinte (3/2), en d’autres termes l’harmonique 3 du son initial, ramenée à l’octave de base. Un déplacement oblique vers le bas d’une unité (par exemple de Do à Mi) indique une transposition d’une tierce majeure (5/4), soit l’harmonique 5 du son initial, ramenée à l’octave. L’angle donné au vecteur de cette harmonique 5 aurait pu être quelconque. Il a été choisi ici d’une part pointant vers le bas par analogie avec les rangées commales basses (-) du clavier Semantic, dans lesquelles il est omniprésent, d’autre part pour aligner verticalement l’axe de symétrie (125/108 – 25/18 – 5/3 – 1/1 – 6/5 – 36/25) des points milieux des 6 familles de sons du système Semantic. L’encadré central rassemble les 36 notes du Semantic Daniélou-36, dont on voit qu’elles couvrent environ quatre des six familles.
Tout intervalle est donc représenté ici géométriquement par un vecteur bien précis, dont la translation en un autre point de la matrice signifie une transposition de cet intervalle. Les possibilités de translation de ce vecteur à l’intérieur de l’ensemble des points d’une échelle donnée détermine les occurrences de cet intervalle dans l’échelle. Cela permet de trouver immédiatement toutes les transpositions possibles d’un intervalle, ou par extension d’un accord, d’une échelle, etc. dans un ensemble donné. Pour prendre un exemple très simple, considérons l’ensemble des points Do Ré Mi Fa Sol La Si. Il se caractérise par une certaine forme, qui résume son identité, et dont nous pouvons déjà vérifier qu’elle contient trois accords parfaits (= triangles de la forme Do Mi Sol). Par translation de cette structure, nous pouvons ensuite trouver toutes ses transpositions possibles à l’intérieur d’un ensemble plus grand, par exemple les 22 shrutis, etc. (il est pratique de s’aider pour cela d’un papier calque, ou d’un transparent, sur lequel on dessinera les structures voulues).
Considérons maintenant le vecteur du comma syntonique (81/80) : il est trouvé entre 1/1 et 81/80 (ou entre les shrutis 5/3 et 27/16, etc.), soit au bout d’un chemin cumulant, dans l’ordre qu’on voudra, 4 quintes (3/2) ascendantes et une tierce majeure (5/4) descendante (un vecteur 5/4 inversé). Ses possibilités de translation entre tous les points de l’encadré intérieur de la figure 4 (correspondant aux 36 sons du Semantic Daniélou) nous indiquent toutes les occurrences du comma syntonique dans cet ensemble, c’est-à-dire 18. Où sont donc passés les six commas manquants, pour arriver aux 24 que compte le clavier ? Ce sont simplement six commas d’un type différent, comme celui séparant Fa# 45/32 de Fa#+ 64/45, soit 2048/2025, dont on retrouvera les emplacements de la même façon par leurs translations.
Pour prendre un dernier exemple, le vecteur du schisma est trouvé entre 256/243 et 135/128. Il est facile ainsi de retrouver les doubles schismiques de toutes les notes nous intéressant, dont seulement quelques-unes ont été représentées dans les encadrés en pointillés de chaque côté des notes initiales. Combien de schismas les ensembles Semantic à 36 ou 53 sons contiennent-ils ? Zéro bien sûr, comme aucun des systèmes ne comprenant pas de notes doubles différant d’un schisma, et dont les périmètres (encadrés de la figure 4) en conséquence sont délimités en largeur par ce vecteur. Attention : les shrutis, représentés ici en gras, sont au nombre de 24 afin de représenter deux très courantes options schismiques (135/128 et 729/512) aux shrutis mentionnés par Alain Daniélou — mais, en regard de leurs variations schismiques, les soi-disant “22” shrutis pourraient être encore plus nombreux.
Une des applications de cette représentation vectorielle, comme on vient de le voir est de pouvoir facilement répertorier et compter le nombre d’intervalles identiques que contient un ensemble de notes. L’intervalle le plus présent du Semantic Daniélou après l’octave est la quinte 3/2 (ou inversement la quarte), avec 31 occurrences. Celles-ci, complétées par 4 quintes faibles d’un schisma, réalisent un cycle continu de 35 quintes de La— à Ré+. La quinte est suivie par le ton majeur 9/8 (ou son complément la septième 16/9) avec 27 occurrences, puis par la tierce majeure 5/4 (comme la sixte mineure 8/5), avec 25. On notera que les deux tierces mineures 6/5 et 32/27 arrivent ensuite à égalité avec 23 occurrences, mais en regard de son double schismique 1215/1024, 10 fois présent, le shruti 32/27 peut être considéré comme la principale tierce mineure. On vérifie aussi que le limma Réb nous laissait indécis à juste titre, étant trouvé 16 fois sous sa forme majeure 135/128 et 15 fois sous sa forme mineure 256/243, et ce quel que soit le choix du limma issu de 1/1. On pourra aussi rechercher de la même façon les intervalles les plus rares du système, afin de pouvoir les retrouver sur le clavier et les expérimenter.
 La représentation vectorielle permet ainsi de saisir très précisément l’origine harmonique de chaque intervalle, la structure de toutes les échelles, et leurs possibles transpositions et variations jusque dans leurs moindres détails. Elle ne donne pour autant pas d’indication directement visuelle de leur ordre de grandeur, ce à quoi la figure 5 permet de remédier. Y sont ordonnées toutes les notes du système global, cette fois sur un cercle dont la circonférence équivaut à une octave logarithmique (soit 1 200 cents, si on utilise cette unité de mesure). Par “logarithmique” on entend une représentation des intervalles sous l’aspect de leurs dimensions relatives. Un même intervalle est ici partout représenté par un même angle d’arc de cercle, quelle que soit sa position dans l’octave, et à des additions ou soustractions d’angles d’arcs correspondent des multiplications ou divisions de leurs rapports de fréquences.
La représentation vectorielle permet ainsi de saisir très précisément l’origine harmonique de chaque intervalle, la structure de toutes les échelles, et leurs possibles transpositions et variations jusque dans leurs moindres détails. Elle ne donne pour autant pas d’indication directement visuelle de leur ordre de grandeur, ce à quoi la figure 5 permet de remédier. Y sont ordonnées toutes les notes du système global, cette fois sur un cercle dont la circonférence équivaut à une octave logarithmique (soit 1 200 cents, si on utilise cette unité de mesure). Par “logarithmique” on entend une représentation des intervalles sous l’aspect de leurs dimensions relatives. Un même intervalle est ici partout représenté par un même angle d’arc de cercle, quelle que soit sa position dans l’octave, et à des additions ou soustractions d’angles d’arcs correspondent des multiplications ou divisions de leurs rapports de fréquences.
Les rapports des 12 touches centrales du Semantic Daniélou y sont reportés en gras, complétés du nom des notes, et celles-ci, avec les notes voisines qui les entourent par le signe – ou +, nous indiquent les 36 sons de l’instrument.
Ces 12 notes chromatiques de base sont séparées par deux types de semitons, 7 limmas et 5 apotomes selon le schéma très classiquement tétracordal suivant : L A L L A – L A L L A – L A. Ces 12 semitons sont ultimement divisés en 4 ou 5 “commas” chacun, parmi lesquels on remarque, dans chaque semiton un comma plus large et coloré ici en gris clair appelé “disjonction”. Les limmas sont donc composés de 3 commas et une disjonction, les apotomes de 4 commas et une disjonction.
D’où viennent ces disjonctions ? Les notes du système d’Alain Daniélou suivent une arborescence (figure 4) qui génère d’abord un « noyau chromatique » central de 12 notes, lequel peut être étendu à d’autres notes différant des premières par un comma, et ainsi de suite. C’est ainsi que l’on passe des 12 notes de base aux 22 shrutis puis aux 36 du Semantic Daniélou et enfin aux 53 du système global, avec lesquels tout l’espace sonore est rempli. L’intervalle restant au milieu de chacun des 12 semitons ainsi réduits successivement de trois, ou quatre commas, est un comma plus grand, un intervalle complexe car reliant des familles extrêmes du point de vue des puissances de 5, auquel on trouve encore ici au même éternel schisma de différence (1,95372 cent) deux expressions, 20 000 / 19 683 ou 3 125 / 3 072. Le premier mesure 27,66 cents et apparait sept fois, le second 29,61 cents et apparait cinq fois. Les commas étant eux-mêmes doubles (de 21,50 ou 19,55 cents), les disjonctions valent donc en moyenne 4/3 de comma moyen.
Comme nous venons de le faire pour les limmas et apotomes, il est maintenant possible à partir de ce cercle d’octave de mesurer et comparer, au schisma près, les dimensions de tous les intervalles du système, en comptant le nombre de commas + disjonctions les composant. On peut ainsi compter dans une tierce mineure 32/27 = 10 commas + 3 disjonctions, et définir de la même façon tout intervalle. Une quarte est composée de 17 commas + 5 disjonctions et une seule exception est trouvée entre FA#- – et Sib++, où l’on compte 18 commas et 4 disjonctions, faisant de celle-ci l’intervalle le plus rare du système, de même que son complément, la “quinte du loup” trouvée entre Sib++ et Fa#- -, mesurant 708,11 cents. On vérifiera en effet dans la représentation vectorielle de la figure 4 l’unicité de ces deux intervalles qui forment la diagonale, intransposable et sans variation schismique possible, du périmètre des 53 sons. On constate ici que le cycle des quintes ne peut reboucler sur lui-même au bout de 53 sons dans le système Semantic sans un écart d’un tiers de comma (un kleisma de 15 625 / 15 552), qu’il est avantageux d’intégrer, pour rendre au Sib++ une quinte aussi correcte que chacune des autres. Cette 54e note est un Fa++ qui peut être au choix 2 187 / 1 600 ou son double 512/375, choisi ici par imitation du choix de 256/225 par Alain Daniélou pour le clavier du Semantic.
Ce Fa++ étant ajouté, nous pouvons entrer à l’intérieur du labyrinthe au moyen de chemins ascendants ou descendants qui chacun vont nous amener en fin de course, à condition de toujours garder la voie du milieu, à une autre note du cercle, une quarte plus haut ou plus bas. Nous pouvons aussi abréger ce long parcours en bifurquant vers d’autres intervalles, comme par exemple en rebondissant à mi-chemin au niveau de deux cercles intermédiaires bien visibles, qui délimitent les intervalles de seconde majeure (9/8) et de tierce majeure (5/4). Tous les chemins sont possibles et nous pouvons aussi nous perdre, ce qui est l’avantage des labyrinthes, pour partir à la recherche d’intervalles plus rares, ou irréguliers du point de vue du nombre de leurs disjonctions, qui nous mèneront jusqu’aux frontières harmoniques du système d’Alain Daniélou.
PHOTOS
Esquisses d'Alain Danielou (5 photos)
Photos : Michel Geiss, Giorgio Pace et Christian Braut