User manual
Summary
- » Introduction
- » The Semantic system
- » Description of the interface
- » First steps
- » Intervals table of the Semantic scale
- » Tunings menu
- » Instruments menu
First steps
Preliminaries :
After opening the UVI Workstation, select “Search” > “Instruments” in the menu (or wherever you will have placed it), then double-click on the “Semantic Danielou-53” instrument to load the program.
Click on any key of the keyboards “Hex” (at the top) or “Hal” (below) to check the sound output and adjust the volume (knob at the upper right).
Activate the “Play” button of the drone (if this drone seems too low in pitch, select one of the two upper octaves in the menu).
Play on either keyboard, Hex or Hal, with timbres and tunings of your choice.
By default, the active tuning is the full scale with 53 notes per octave “Semantic-53”.
On the “Hal” keyboard (with piano keys), the default tuning spans the 53 degrees of the Semantic scale starting from C2 and extends them by octaves, in their pitch order.
In alternative, the tuning “Semantic-45” reiterates the note 1/1 with every C key in order to make it easier, for first encounters if you use a external MIDI keyboard, to play 45 of the main intervals of the Semantic scale with 1/1, which will be repeated in the higher octave with the same fingerings.
Refer to the list of tunings (in teh supporting documents) to visualize their classification by types of tunings.
Notes forming an heptatonic scale are are generally placed on the white keys of the Hal keyboard (below), while all 12 notes of the scale are on the white + black keys (= higher rank of the Hal keyboard).
For example, in the tuning menu, select any of the Indian ragas situated between Ahir Bhairav and Todi, and slide on the keys of the Hal keyboard to feel their special “rasa” (feeling), or follow the suggestions of specific experiences among those suggested in the following pages.
Presentation of the buttons keyboard “Hex” of the Semantic Daniélou-53 :
This mapping of the 53 notes of the Semantic in 7 diatonic columns, changing their color at middle-height, respects the classic “Halberstadt” form with 12 white and black keys par octave borrowed by the original Semantic, while displaying a continuous succession of commas vertically. The hexagonal keys here have the advantage of making the difference between major tones (9/8) and minor tones (10/9), being tempered to one unique value in the Western meantone tuning while in the Semantic system (as in Indian music and in every other just intonation system) they differ by a comma.
With this special form of keyboard, not only can the vectors of the major or minor tones be clearly differentiated at a commal level, but also the vectors of any class of interval (such as the minor thirds, fourths, fifths, sixths, and any shrutis), as well as all tetrachordal forms, etc. which use them. (See the honeycomb display of the Semantic-53 scale).
Any pure fifth, for example, sees its keys aligned horizontally in the same way, which was not possible with a non-hexagonal keyboard. Respecting these isomorphisms, the geometry of a major diatonic scale becomes :
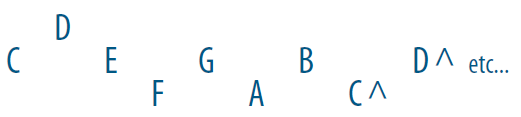
It is also exactly the lower keys pattern of the Axis keyboard, which can serve as an additional visual and tactile help.
Around the middle-height of the keyboard, the color change between the “white” and “blacks” zones of every column operates at the level of the disjunction, shown by a yellow colored line.
(Note that when used with any tuning of 12 notes per octave, the yellow lines of the Hex keyboard indicate the shift to the following note of the scale).
One note about the mapping of the tuning by default Semantic-53 : the Axis-64 keyboard consists of 64 notes arranged by octave, there are 11 occurrences of the Semantic-53 notes on the Axis-64, and on the interface’s Hex keyboard they are repeated the same way at each octave. These are: 100/81, 320/243, 4/3, 27/20, 512/375, 40/27, 400/243, 80/81, 1/1, 81/80, 250/243, which facilitate the ergonomy of some fingerings.
As a purely esthetical difference between the Axis-64 keyboard and the interface’s Hex keyboard (besides the extension of the Axis range to 3 full octaves), on the interface, Hex keyboard columns of keys show one slight angle, which allows to align vertically the upper key of a column with the lowest key of the following one.
EXERCISES :
1st experience : Major diatonic scale (raga Bilaval) from the Hex keyboard.
Play a major diatonic scale in the low part of the Hex keyboard on keys 1/1 – 9/8 – 5/4 – 4/3 – 3/2 – 5/3 – 15/8 – 2/1 (see the pattern above).
Learn to find in this scale the intervals you are familiar with, for example :
2/1 = octave
3/2 = fifth
4/3 = fourth
5/4 = major third
5/3 = major sixth
15/8 = major seventh, etc.
Take time to experience the just intonation sound qualities, perhaps new to your ears, of the thirds, sixths and major sevenths.
Notice that the thirds (5/4) and fifths (3/2) are lined up on the same horizontal rows (perfect triads [C : E : G], [F : A : ^C], or [G : B : ^D]), and that the Hex keyboard differentiates the major tones (9/8) found between 1/1 and 9/8, 4/3 and 3/2, 5/3 and 15/8, using an ascending fingering, from minor tones (10/9) found between 9/8 and 5/4 or 3/2 and 5/3, using a downward fingering.
2nd experience : Minor diatonic scale (Eolian mode, raga Darbari, etc.) and comma genesis.
Let us first learn to tune the programmable drone in another pitch, here in A (5/3) instead of C : let us look for this pitch in the Intervals table of the S-53 scale : we find it in the 39th comma where its value is given in thousandths of cents, 884.359. The Semantic drone has a precision of a hundredth of a cent, so we shall enter the value 884.36 in the pitch field.
Play again the same notes as in the previous exercise and listen well to the chords they create with the drone. Notice that the relative tone A (5/3) is perfectly consonant with all the notes of the scale, except one, 9/8 (D) to whom we may prefer 10/9 (“D -” according to Alain Daniélou’s writing) presenting now an interval of a perfect fourth with the drone:
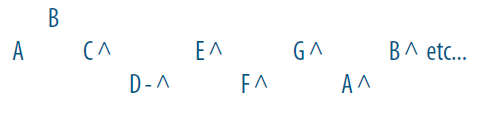
(Note that this geometry of keys from A is identical to that of the major scale from C)
With two necessary values differing by a comma for the interval of a second in the diatonic scale, we have gone back to the sources of the original meantone temperament, which in alternative to a double note for the major second (D and D-), has chosen an average intermediate tone (or ” meantone “), which was the starting point of all baroque temperaments, up to the actual western 12-equal temperament. This double option of the second interval is valid for any note in other keys. To express all the harmonies of the chromatic scale in just intonation, we then need more than 12 notes per octave, such as the 22 indian shrutis (see experience # 22).
You may also try the ” Pramana “scale (demonstration tunings) which cumulates the commal variations of a diatonic scale by displaying them by successive perfect fifths from F (4/3), or D – (10/9).
Alternatively you may play in a minor mode identical to the Eolian mode, with the tuning “Darbari” (Indian ragas), whose commas positioned on the minor notes allows to modulate them creating expressiveness (such inflection effects are found in some “gamaka” ornaments of indian music).
3rd experience : Minor pentatonic scales with 2 semitones
(defective scale of the previous Eolian mode, in another key)
Tune the drone to 498.04 cents to obtain F = 4/3
Play in the higher part of the Hex keyboard the notes :
1/1 – 16/15 – 4/3 – 64/45 – 8/5 – 2/1 – 32/15
Also with two semitones and in the same tonic (4/3), a variant is the pentatonic Gunakri raga :
1/1 – 16/15 – 4/3 – 64/45 – 16/9 – 2/1 – 32/15
Feel how a heptatonic scale (the Eolian mode) and various defective versions of it can arouse different emotions.
4th experience : Chandrakaus raga
Again with a drone of 498 cents, in order to have the “Madhyama” (note F = 4/3) as the tonic.
Dedicated to Chandra (the Moon), this very popular evening raga, in “Madhyama” tuning (without the fifth “PA”) is obtained on the Hex keyboard with notes :
1/1 – (32/27 and 6/5) – 4/3 – 8/5 – 15/8 – 2/1
5th experience : “Harmonic” minor scale, on the Hex keyboard
The so-called “harmonic” minor mode, can be summarized as an Eolian mode with a major 7th in place of the 7th minor, in other words with a major third above the dominant, hence its common western name. Depending on the schools several commal variations of the scale can exist, such as in the Indian ragas themselves Kirwani (North India) or Kiravani (South India) ; it is also an ancient version of the Pilu raga (North India). The scale presents numerous other modes and variations found in Eastern Europe music (gypsy scales) as well as in Indians ragas (Basant Mukhari, Madhuvanti, etc.).
To experiment with these various options, let us tune at first the drone to 320/243, with a pitch of 476.54 cents. On a horizontal line in the second half of the Hex keyboard we find a minor triad with notes : 320/243 – 128/81 – 160/81 ; whereas the major triad of the dominant note (PA) will be found in the bottom row of the keyboard : 80/81 – 100/81 – 40/27 (note that these two last notes are also repeated at the very top of the Hex keyboard).
The other major triad of the scale is : 135/128 – 320/243 – 128/81.
The complete scale is thus played on keys :
135/128 – 100/81 – 320/243 – 40/27 – (128/81 – 25/16) – 225/128 – 160/81 – (25/16 – 135/64) – 200/81 – 640/243.
Its commal variations concern mainly the minor notes, which can be lowered of a comma in their own column, that are 25/16 and 25/12, which act as minor thirds of a “19/16” type above SA and MA, which remain unchanged. But the major seventh (the “leading tone”) 100/81 could also be raised by a comma, with the note 5/4, to form a pure major third with 25/16. In an optional complement such as in Pilu raga, a 7th minor (of a 16/9 type) in tune with 25/16 and 25/12 will be found in 75/64.
6th experience : Harmonic minor scale, pre-programmed (tuning Kidarvani)
Select this time the tuning ” Kidarvani ” (contraction of ragas “Kirvani” and “Darbari”).
The scale, which contains several of the variations suggested in the previous exercise is the following one :
1/1 – 9/8 – 19/16 – 6/5 – 4/3 – 3/2 – 8/5 – 16/9 – 9/5 – 15/8 – 2/1
It can be experimented as well on the Hex keyboard as on the Hal keyboard, with a drone in C.
7th experience : Mougi raga
In the lineage of the previous modes, this raga with gypsy consonances (composition of Jacques Dudon) takes advantage of the Semantic-53 full scale keyboard to suggest slidings by descending commas between each of the 4 semitones. The main notes of the scale, which uses F# instead of F are the following ones :
1/1 – 9/8 – 19/16 – 45/32 – 3/2 – 16/9 – 15/8 – 2/1
It will be interpreted preferably on the Hex keyboard with a drone tuned in C (zero cents).
The slidings can be played by patterns of 6 descending commas each, starting from notes 2/1, 256/135, 3/2, 6/5.
For a more basic version adapted to the Hal keyboard, select the tuning ” Mougi-c “.
8th experience : Five-limit Bhairav raga
Again on the Hex keyboard with a drone in C, this morning raga, considered as the king of ragas and an expression of Shiva is approached in 5-limit by the notes :
1/1 – 16/15 – 5/4 – 4/3 – 3/2 – 8/5 – 15/8 – 2/1
A beautiful defective form of this raga is the very ancient pentatonic Bibhas raga:
1/1 – 16/15 – 5/4 – 3/2 – 8/5 – 2/1
9th experience : Bhairav Raga, in 17-limit
The scale, Bhairav-17, in the tuning menu suggests a pre-tuning of the keyboards in which vadis and samvadis (main notes of the raga) contain optional semitones 17/16 over SA (1/1) and PA (3/2), perfectly coherent with the Bhairav mode and providing a very sweet kleisma (256/255) beating with their alternatives of 16/15. With attentive listening we can distinguish a subtle difference of feeling between the semitones 17/16 and 16/15, the first ones much more steady, detached, contemplative, the second ones more emotional and passionate.
By sliding at the level of the blacks keys on the Hal keyboard we sweep all the notes of the raga in an effect that recalls the sympathetic strings of the sitar, or those of the “swirmandal”, a zither often used in hindustani vocal art.
10th experience : From Eratosthene’s schisma to the Todi raga
The ” Eratosthenes ” scale (in the “Demonstation tunings” family) shows how a sequence of 5 perfect fifths (3/2) over 5/4 ends in a third minor of 1215/1024, one small schisma (1216/1215) under 19/16. By disregarding 5/4 (the F key here), this cycle, completed by SA (1/1) and PA (3/2), generates all the notes of the Todi raga.
In a more appropriate mapping, we can experience a completely coherent version of the illustrious Thaat raga Miyan Ki Todi with the tuning “Todi-c” (“Indian ragas” family).
The very popular raga “Gujari Todi” uses the same scale without the note PA (3/2).
11th experience : Chromatic scale “Coherent_shrutis”
This selection of 12 of the 22 shrutis (cycle of fifths from A to D), thanks to the 19th harmonic presents an optimal differential coherence with 1/1, therefore, a better consonant quality. It suggests a special chromatic scale in the minor mode for the interpretation, among others, of numerous ragas (Bhairavi, Mishra ragas, and most ragas from the Ghazal, Qawali and Thumree styles) :
1/1 – 19/18 – 9/8 – 19/16 – 5/4 – 4/3 – 45/32 – 3/2 – 19/12 – 5/3 – 16/9 – 15/8 – 2/1
12th experience : Marva raga
In a classic modeling in 5-limit, its shrutis would be selected among the 22 shrutis scale (Semantic sets) – the following indicates what could be the notes of this typically Indian raga, played by the setting sun, which omits the note PA (3/2) :
1/1 – 135/128 – 5/4 – 45/32 – 27/16 – 15/8 – 2/1
But it reveals, however, some uncertainties concerning the notes GA, DHA, NI (= E, A, B), in particular, because of a dissonant fourth here between E and A. Taking advantage of some of the intervals of the “Coherent shrutis” scale, obtained notably from a tonic in 19/16, the “Marva-c” tuning optimizes the differential coherence of all intervals, by doubling each of its shrutis:
1/1 – 20/19 – 17/16 – 5/4 – 24/19 – 45/32 – 27/19 – 5/3 – 32/19 – 15/8 – 36/19 – 2/1
We may notice that the Marva mode contains a complete pentatonic scale of a Bhupali type from Dha (32/19).
13rd experience : Bayati
One of the most popular modes of the Arabic music is certainly Bayati, originally a tetrachord of 13-limit which can be approached in a beautiful way by dividing a fourth in 20 – 22 – 29 kleismas found with the Semantic intervals :
1/1 : 625/576 : 32/27 : 4/3
We find them for example from the note 256/225 (223.46 c.), which we can tune the drone in.
The keys of the Bayati tetrachord to be used are then :
256/225 : 100/81 : 27/20 : 243/160
which we can extend by a second identical tetrachord :
128/75 : 50/27 : 81/40 : 512/225
Do not hesitate to raise the release level of the envelope as much as you want to enjoy all the oriental flavor of the small and large neutral seconds (625/576 and 2187/2000, respectively 20 and 22 kleismas) of the scale.
14th experience : Slendro scale of central Java (on the Hex keyboard)
This 5-limit slendro, but of septimal colors, is found with notes
128/125 – 75/64 – 4/3 and/or 27/20 – 192/125 – 225/128 – 256/125
Optionally, a very soft drone tuned on 75/64 = 274.58 cents may be used. It may be used in option with a very soft drone tuned on 75/64 = 274.58 cents.
The syntonic comma between 4/3 and 27/20 here occupies an arbitrator’s place, completely reversing the scale in function of the chosen note ; we shall notice that although having the size of a comma, it is virtually perceived in this context as a semitone.
Note also the very strong consonance of the chord 75/64 : 225/128 : 256/125 which will quite naturally be interpreted as a basic overtones 4 : 6 : 7 triad.
15th experience : Approximation of a Javanese Slendro in 5-limit
Select the “Slendro_cloud” scale of the tuning menu (excerpted from the Semantic-36 scale and without pure septimal tones), to be played with the “Xylo” instrument and on the Hal keyboard :
1/1 – 729/640 – 675/512 – (3/2 and/or 243/160) – 225/128 – 2/1.
Each of the 6 notes is doubled in the higher octave, placed on its next key.
16th experience : Slendro matrix
The “Slendro_sequence” scale of the tuning menu suggests this matrix / collection of typically Javanese circular Slendro scales, of triseptime type (= containing 3 septimals tones 8/7 or 5-limit equivalents per octave), the just intonation version of a sequence of 69 kleismas (171ths of octave), such as 250/189 here (C : F) :
1/1 – 81/80 – 8/7 – 125/108 – 75/64 – 250/189 – 75/56 – 189/125 – 49/32 – 3969/2560 – 7/4 – 567/320 – 2/1
Immerse yourself in the specific consonance of the septimal tone (8/7), found in multiple places. (to be experimented again with the “Xylo” sound…)
17th experience : Harmonics (World musical cultures)
The scale of natural overtones is present in number of instruments such as the Jew’s harp, the African mouth bow, the didjeridoo, and of course the voice (vowels singing, overtone singing, polyphonies…).
The tuning ” Harmonics ” browses on each octave from C to C^ the natural harmonics from 12 to 24 :
12 – 13 – 14 – 15 – 16 – 17 – 18 – 19 – 20 – 21 – 22 – 23 – 24
It allows therefore the experience of intervals of various limits, and in various modes.
With a drone tuned in 4/3 (= E key) at first we can simply feel the energy communicated by each of these harmonics in their pure state.
With the default drone C (= harmonic 12 here) then by using alternately every harmonic as a tonic, we can explore which feelings it brings to each of the other harmonics (this experiment is valid for every note of any scale).
If we wish to tune the drone in the Semantic in unison to a given note, it is necessary to enter its value in cents, given by the formula: Log (ratio) / Log ( 2 ) * 1200. The last number is the number of units by octave, here 1200 cents.
The ratios of the notes with the reference note C = 1/1 are here :
13/12 – 7/6 – 5/4 – 4/3 – 17/12 – 3/2 – 19/12 – 5/3 – 7/4 – 11/6 – 23/12
For example, to tune the drone to the first interval (13/12) with 1/1, we shall enter the value :
Log (13/12) / Log ( 2 ) * 1200 = 138.572661 c.
18th experience : Thai scales (World musical cultures)
The very original, and harmonically mysterious traditional scales of the Siamo-Khmer music are often presented by the musicologists as “quasi-equal” heptaphones.
The “Thaï_17l-tetrac” tuning, from intervals stemming from the global canvas of 171 kleismas generated from the Semantic-53 scale, achieves a realistic modelling of a Thai heptaphone, designed from two tetrachords a meantone fourth 75/56 wide, divided into 3 quasi-equal intervals, of a 75/68 type or equivalents : 1/1 – 193/175 – 75/68 – 17/14 – 1277/1050 – 75/56 – 11269/8400 – 112/75 – 4607/2800 – 288/175 – 2901/1600 – 136/75 – 2/1
The triad 56 : 68 : 75, with the very strong differential coherence of the Thai tone 75/68 (because 75 – 68 = 7), shows the interest of the kleismic extension of the Semantic scale, applied here to South-Asian music.
So this scale consists of 6 tones of this type and a wider tone of the meantone type in the middle, between F and G, thus containing no “semitone”.
The scale “Thai_reversible”, in another series, adds three commas, inverting the positions of the 11/10 and 10/9 types of intervals, and also proposing an optional neutral tone of a 12/11 type between E and F.
Compare these previous Thai scales with those of the tuning “Siamese_7-qedo”, getting closer to an “almost equal” division of the octave in 7 (generator of 128/105, or 49 kleismas, borrowed from the “Yantra”scale).
Experience diverse pentatonic modes selected among these various scales.
19th experience : Kleisma coincidences
Select the tuning “Kleisma” (in Demonstration tunings).
The scale assembles two sequences of minor thirds (6/5), seven starting from 5/3 and three others starting from 125/72, producing low fifths (23 328 / 15 625) of a 5-limit kleisma (15 625 / 15 552) or 8.107278862 cents.
The four kleismas found in C#, E, G, A# make it possible to recover 3 perfect major thirds (5/4) and a perfect fifth (3/2) :
1/1 – 648/625 – 25/24 – 6/5 – 3888/3125 – 5/4 – 36/25 – 23328/15625 – 3/2 – 5/3 – 216/125 – 125/72 – 2/1
Afterwards, with the full scale of the Semantic-53 (default tuning) on the Hex keyboard, you may exercise your listening to make the difference between intervals situated entirely in one of the zones between the two yellow lines, and their “kleismic variations” of equivalent fingerings but straddling on both sides of a yellow line. These kleismic variations are listed in the “Intervals table” of the Semantic scale.
20th experience : Schisma (Demonstration tunings)
Going down 8 perfect fifths (3/2) under D (9/8) we obtain (1024/729, on the F key here) a 3-limit third, while a perfect major third (5/4) above D (45/32, on the F# key) gives a note a schisma higher (5*3^8/2^15 = 32 805 / 32 768).
The scale, in the ascending order of the keys, progresses by perfect fifths transposed back into the same octave, which produces a surprising melodic effect :
1/1 – 3/2 – 9/8 – 27/16 – 81/64 – 1024/729 – 45/32 – 256/243 – 128/81 – 32/27 – 16/9 – 4/3 – 2/1
21th experience : Ragisma (Demonstration tunings)
The ragisma is simply the archetypal footbridge allowing to express a 5-limit interval in its equivalent in 7-limit, and vice versa. Seven perfect fifths (3/2) and an octave (2/1) above A here end in a note, one ragisma lower than the 7th harmonic of the note found after four perfect major thirds (5/4) above the same initial A. The ratio of this remarkable micro-coincidence is 4 375 / 4 374, that is 7 * (5^4)/2 * (3^7).
This strange scale here is a “Dudon scale” of this coincidence (= gathering all the divisors of its numerator and denominator :
1 3 5 (7) 9 25 27 (35) 81 125 (175) 243 625 729 (875) 2187 (4375),
then transposed to the same octave.
While this full scale would need 17 notes, in the simplified 12 notes version of this tuning, we can cover all the series of fifths and thirds. We can’t listen to both versions of the coincidence, rather difficult to distinguish by ear, since the notes 4374 : 4375 are even closer than those of the Yantra schisma 4095 : 4096 (see experience 28).
However, we can appreciate, and in a optimal way with oboe, saxophone or clarinet timbres, the strong consonance of the 5-limit version of the 7/4 interval, that is 2 187 / 1 250, between keys C and Bb.
22nd experience : The 22 Indian Shrutis
The tuning ” 22 shrutis ” (Semantic sets) enables a complete experiment of this reference scale of both North and South Indian music, which without transposition provides a correct rendering of all ragas. The intervals between the 22 notes alternate commas and intermediate semitones of two sizes, the lagu (found for example between the minor third 6/5 and the major third 5/4) and the limma (for example between the tone 9/8 and the 3-limit minor third 32/27).
Two additional notes above and below 1/1 allow the experiment of the schisma between 256/243 and 135/128 (and reversed), quite subtle to differentiate – to play them together will make you appreciate the slowness of their beating.
23rd experience : Syntonic comma pump
With the tuning S-53 on the Hex keyboard, a series of 5 consonant notes, for example played two by two help to experiment the genesis of the syntonic comma, here between C and C+ :
C : G : D : A+ : E+
G : D : A+ : E+ : C+
(1/1: 3/2: 9/8: 27/16: 81/64: 81/80 etc.)
It is what is called a “comma pump”.
Its continuation can be transposed easily by ascendent degrees on the Hex keyboard (down more or less to the kleisma) to perform this pump in a loop and generate a continuous spiral of ascending commas :
C+ : G+ : D+ : A++ : E++ >
C++ … etc.
The same path can be performed backward to generate a continuous series of descending commas.
24th experience : Amlak (World musical cultures)
Halfway between Ethiopian music and some night Indians ragas, this fascinating mood scale is the result of the deployment of the fractal algorithm x^2 = x + 1/3, performed here by the frequencies 27 – 36 – 45 – 57 – 72 – 91 – 115 … which trends towards a series of wide major thirds, allowing among other things to link in a coherent way major sevenths and minor thirds (ex : 57 – 45 = 9, etc.) :
1/1 – 45/38 – 19/16 – 91/76 – 107/76 – 27/19 – 455/304 – 3/2 – 30/19 – 575/304 – 36/19 – 2/1
If you enjoy this scale, in quite similar colors but appreciably more Indian you can also experiment the “Nila” raga (Indian tunings) :
1/1 – 17/16 – 16/15 – 19/15 – 4/3 – 8/5 – 101/60 – 19/10 – 2/1
Or also the very hieratic “Shri Rag” (Indian tunings), to be interpreted on winter after sunset, here modelled as well according to an Amlak series, to optimize its differential coherence.
25th experience : Semantix-36 (Related temperaments)
The interval of 27/25, known also under the name of “Zarlino semitone”, used as generator, divides the octave almost exactly into 9 intervals of 19 kleismas each, with the property that if we double this interval, or 729/625, the result is indistinguishable, in practice, from a septimal minor third 7/6 (the difference again is a ragisma, 4 375 / 4 374).
This enneaphone, thus built advantageously by alternating 27/25 and 175/162, and transposed by 9/16, 3/4, 1/1, and 4/3 (a series of perfect fourths) ends in a 36 notes per octave “harmonic temperament” particularly rich in footbridges between the 5 and 7 harmonics :
1/1 – 49/48 – 25/24 – 200/189 – 27/25 – 54/49 – 9/8 – 8/7 – 7/6 – 25/21 – 243/200 – 100/81 –
63/50 – 9/7 – 21/16 – 4/3 – 49/36 – 25/18 – 567/400 – 36/25 – 72/49 – 3/2 – 49/32 – 14/9 – 100/63 –
81/50 – 81/49 – 42/25 – 12/7 – 7/4 – 25/14 – 49/27 – 50/27 – 189/100 – 27/14 – 96/49 – 2/1
Its successive notes have between them a pattern of intervals repeated in a loop of [ 5 – 5 – 4 – 5 ] kleismas, of an average of a sixth of a tone, that suggests an interesting alternative to the 36 notes per octave equal temperament, which has been used by numerous composers in the last century.
The Indonesian Pelog scales being commonly considered for being defective scales of divisions of the octave in 9 intervals, the Semantix-36 scale then contains 36 various versions of Pelog scales.
The 12 notes tuning Semantix-12 proposes some of them in C, G, B, as well as on its white keys a diatonic scale which could very well suit the tuning for an African cora or a Malagasy vali, with two “wide semitones” of the 27/25 type.
The keys C C# D# (and G G# A#) reproduce the notes 27/25 and 7/6 with the almost identical intervals 27/25 and 175/162 between them.
The notes C C# E F (or a fifth above G G# A C^) suggests a rather realistic variation in 5-limit of the ancient medieval Persian tetrachord “Buzurg”.
As for the tuning “Semantix-Semantic”, entirely in 5-limit, but being of very middle-oriental colors, it offers a selection of the intervals common to the scales Semantic-36 and Semantix-36. On the white keys, it is an interesting variation of the previous diatonic scale, 400/243 in A instead of 42/25 :
1/1 – 27/25 – 9/8 – 243/200 – 100/81 – 4/3 – 25/18 – 3/2 – 81/50 – 400/243 – 729/400 – 50/27 – 2/1
26th experience : the Tsaharuk scale
Stemming from the scale S-53, a neutral second interval of 20 kleismas (see in interval table : 625/576, 243/224, or 64/59, 13/12, etc.) has the property of being precisely the fifth of a perfect fifth (3/2, 100 kleismas), as well as the sixth of a neutral sixth (13/8, 120 kleismas). Nothing surprising thus that when used as a generator it produces numerous familiar intervals used in Arabic music.
In the Semantic system we find this interval in numerous places, for example between one low semifourth (144/125) and a major third (5/4).
Its cyclic properties lead us to suggest a generalization of the qanûn tunings systems of the late Arabic music master Julien Jalaleddin Weiss, who used up to 105 notes per octave to interpret, in just intonation, all the subtleties of various Arabic music schools and traditions.
One version with perfect fifths of this harmonic temperament verifies the equal beating of both intervals 13/12 and 16/13 of the triad 12 : 13 : 16, expressed in the algorithm 8x^6 – 13 = 12x – 13.
From the Tsaharuk-12a twelve notes tuning (World musical cultures),
1/1 – 755/696 – 296/261 – 273/232 – 107/87 – 4/3 – 755/522 – 3/2 – 755/464 – 148/87 – 819/464 – 107/58 – 2/1
adjust a drone in 217.86 c. to experiment a Bayati mode on white keys from D (296/261).
From the Tsaharuk-12d tuning, reset the drone in C = 0 c. to experiment a Rast mode on white keys from C (1/1).
Alternately, Tsaharuk-17 and Tsaharuk-24 tunings (Related temperaments) show two different aspects of the complete parametrable system, presenting balanced divisions in 17, 77, 94 or 171 notes per octave. One is closer to Persian music for the 17 notes scale, the other one to Arabic music for the 24 notes scale (they are both displayed on 24 notes on the Hal keyboard).
The scale of the Tsaharuk-24 tuning consists of two sequences of 11 schismatic fifths transposed by a triple comma (typ. 28/27) :
1/1 – 28/27 – 59/56 – 35/32 – 9/8 – 7/6 – 32/27 – 59/48 – 5/4 – 35/27 – 4/3 – 112/81 – 59/42 –
35/24 – 3/2 – 14/9 – 128/81 – 59/36 – 27/16 – 7/4 – 16/9 – 59/32 – 15/8 – 35/18 – 2/1
27th experience : Mohajira-to-Slendro (World musical cultures)
Mohajira is at the same time a very ancient tetrachord mentioned by Ibn-Sina, a scalar structure, a very rich family of fractal scales, and a linear temperament having for generator a neutral third, typically close to 11/9. The scale in 12 notes suggested here :
1/1 – 21/20 – 9/8 – 6/5 – 49/40 – 4/3 – 7/5 – 3/2 – 8/5 – 49/30 – 9/5 – 11/6 – 2/1
comes from the harmonic coincidences 539 : 540 and 440 : 441, found in the neutral thirds series of the Mohajira sequence :
80 – 98 – 120 – 147 – 180 – 220 – 270
of which the characteristic heptaphonic structure is displayed here on the white keys of the Hal keyboard, beginning with note G : it contains three Mohajira tetrachords, of simplified quartertones form : [3 – 4 – 3] from G, B and D.
The scale also presents an Eolian mode in C minor, and many Slendros (pentatonic Indonesian scales),
such as a typical slendro from Jogyakarta in E F# G# B C#,
another one between Surakarta and Jogyakarta slendros in C# Eb F# G# B,
another one of a traditional form of central Java in E F# A B C#,
or another one of a simpler form, on the 5 black keys.
Thus it makes it possible to link musical cultures very distant at first, therefore its name “Mohajira” which means “migrant”.
28th experience : Yantra schisma (Demonstration tunings)
This 12 notes scale is again a “Dudon scale” (= collecting all the divisors of the numerator and the denominator of a harmonic coincidence, transposed in the same octave) of the micro-schisma 4 095 : 4 096, with factor 35 left here undivided :
1 3 9 13 35 39 105 117 315 455 1365 4095
One can experiment the smallness of this schisma by playing simultaneously keys F# and C^ to listen to their beating.
Its name comes from the fact that the logarithmic representation of this scale in an octave circle allows a geometrical construction of the very famous and mysterious “Shri Yantra” mandala, thanks to very strong symmetries which it establishes between its ratios based on the harmonic 13 :
13, 39, 117 and their symmetrical “quasi-complements”, multiples of the factor 35 : 315, 105, 35 …
Apart from for this singular property, this scale contains a number of modes which can be related to Arabic music and quoted by the ancients, such as a Rast mode in F, a Bayati mode in G, two Mohajira scales in C (tetrachords 1/1 – 35/32 – 39/32 – 1365/1024 and 3/2 – 13/8 – 117/64 – 2/1) and in neutral E (39/32 – 1365/1024 – 3/2 – 13/8, etc.), with two commal options in E and A and two additional symmetrical quartertones in D and Bb.
It can be appropriate to experiment it with a long sustain, to fully enjoy the flavors of its differential consonances, along with an optional drone in G (3/2 = 701,955 c.), or other notes to one’s choice.
29th experience : Kleismean (World musical cultures)
The Semantic system, extended to its “ultimate” deployment in 171 kleismas, allows the simulation of various meantone temperaments, irregular temperaments, well-temperaments, etc., from rational intervals. The “Kleismean” harmonic temperament proposed here fulfills, in 7-limit and by a specific irregular alternation of perfect fifths (3/2) and smaller ones (typically 112/75, flat by a kleisma), the imitation of a meantone temperament presenting perfect major thirds (5/4) at the end of a series of 4 fifths, without ever presenting fifths low of a comma, and by leaving on the other hand on the extremities of the fifth chain as in any meantone temperament, a “fifth of the wolf ” (of 32/21 here) between G# and Eb^ :
1/1 – 21/20 – 28/25 – 448/375 – 5/4 – 75/56 – 7/5 – 3/2 – 196/125 – 375/224 – 25/14 – 15/8 – 2/1
It will be interesting to compare the global tuning coherence of the white keys of this type of scale, versus the pure consonance of the white keys of adiatonic scale of more classic just intonation (such as those of “Semantic-12” or of “Coherent shrutis”) ; this accuracy sensation depends obviously on our kind of listening but also on the acoustic, harmonic and musical context of the moment.
30th experience : Semantic_Axis-19 (Demonstration tunings)
A meantone scale, tempered “to a third of a syntonic comma” possesses perfectly pure major sixths (5/3) and minor thirds (6/5), a characteristic that is shared with the Semantic scale.
Extended beyond 12 notes this historic temperament generates a scale of 19 tones, always very popular among microtonal musicians.
A meantone scale has two sizes of semitones (said “chromatic” for the smaller, “diatonic” for the larger) and a single type of a major tone, which will sum up, in a scale of 19 notes per octave, to three degrees. Therefore the origin of our western classical notation with sharps and flats, a C# not being originally equivalent to a Db, before they became identical with the 12-equal temperament.
The difference, of 9 kleismas between the two semitones in a scale of 19-equal, among the largest in the various meantone forms, is part of its particular flavor.
Contrary to a number of notes limited to 12 for a meantone scale, there are no “forbidden chords” in 19-equal, which offers full circular harmonies.
The extension of the Semantic system ending up in 171 thirds of commas (or kleismas) per octave, and this number being a multiple of 19, there are 9 possible manners, from intervals multiples of 9 kleismas, to generate by reiteration harmonic scales in 19 “quasi-equal” tones in this extension. Five of them already belong to the Semantic-53 scale : 648/625 (9 k), 125/108 (36 k), 6/5 (45 k), 3888/3125 (54 k), and 25/18 (81 k).
Not less interesting, the four others are issued from the precedents, these are 672/625 (18 k), 125/112 (27 k), 4032/3125 (63 k), and 75/56 (72 k).
(In the second half-octave the next generators to be multiples of 9 kleismas will be equivalent to the inverses of the precedents).
To stay as closely as possible to the Semantic scale, the repetitions of perfect major sixths and minor thirds have been favored here, sometimes by simplifying their ratios (ex. 56/45 instead of 3888/3125, etc.) :
1/1 – 28/27 – 672/625 – 125/112 – 125/108 – 6/5 – 56/45 – 4032/3125 – 75/56 – 25/18 – 36/25 – 112/75 –
3125/2016 – 45/28 – 5/3 – 216/125 – 224/125 – 625/336 – 27/14 – 2/1
31th experience : Semifourths
After the division, the most frequent in traditional world music, of a minor third in two “3/4 of tone”, another way of generating quartertones is observed in Africa in diverse pentatonic balafon tunings, generally dividing three of its fourths (4/3) into two “semifourths”.
The tuning “Bala_sem-sem” (World musical cultures) contains several versions, in G and in A, of traditional tunings of pentatonic balafons from Mali and Burkina Faso used for celebrations, chaining 4 semiffourths, translated in 5-limit by alternation of semiffourths 108 : 125 (36 k.) and 125 : 144 (35 k.) to generate a series of fourths.
As for the tuning “Bala-ribbon” (Related temperaments), it interleaves two “Bala” fractal sequences :
1/1 – 25/24 – 9/8 – 6/5 – 13/10 – 4/3 – 83/60 – 3/2 – 8/5 – 26/15 – 9/5 – 39/20 – 2/1
The black keys reproduce a pentatonic sequence of semifourths similar to those of Bala_sem-sem :
[108 : 125 : 144 : 166 : 192] (where 108 is here in Bb).
The second Bala sequence, displayed on the white keys :
[117 : 135 : 156 : 180 : 208 : 240 :(277): 160] is containing two others from 117 in B and from 135 in D.
By coincidence, this “ribbon temperament” also recomposes a full 5-limit Eolian mode from C (1/1) :
1/1 – 9/8 – 6/5 – 4/3 – 3/2 – 8/5 – 9/5 – 2/1
Explore in this Bala-ribbon tuning the possible migrations of the diverse African pentatonic modes between them, and towards this Indo-European mode.

